문제

풀이
처음에 생각했던 방법은 완전 탐색을 통해 최대 수를 찾는 방법이었다. 중간에 가지치기를 통해 시간을 줄일 수 있겠지만 n의 최대값이 100이고 (모든 점에 대해 놓는 경우/ 놓지 않는 경우) * (놓을 수 있는지 판단하기 위해 양 대각선을 탐색하는 경우)를 하게 되면 O(2^n * n)이기 때문에 시간초과가 발생할 것 같아서 다른 방법을 생각해봤다.
생각한 방법은 N-Queens에서 모든 행렬을 저장하지 않고 해당 idx에는 하나의 값만 올 수 있도록 한다면 시간을 줄일 수 있다는 생각을 했고 데이터를 어떻게 묶어야 할지 고민을 해봤다. N-Queens에서 queen은 가로,세로를 갈 수 있었고 이로 인해 하나의 행에 퀸을 놓을 경우에는 같은 행에는 퀀이 존재하지 못하는 성질을 이용했었다. 이와 유사하게 대각선을 하나의 집합으로 묶어서 처리했다. 이 집합은 cache라는 배열로 2N - 1개의 대각선이 존재하므로 크기는 2N - 1으로 설정, 저장하는 값은 해당 대각선에 놓는 점의 X좌표를 저장하였다. 해당 방법을 이용하게 되면 각 대각선에 어디에 놓을지 결정하는 것과 같기 떄문에 O(n * (n-1)!)의 시간 복잡도를 가지고 실제로는 가지치기를 통해 더 적은 경우의 수를 탐색할 수 있다.
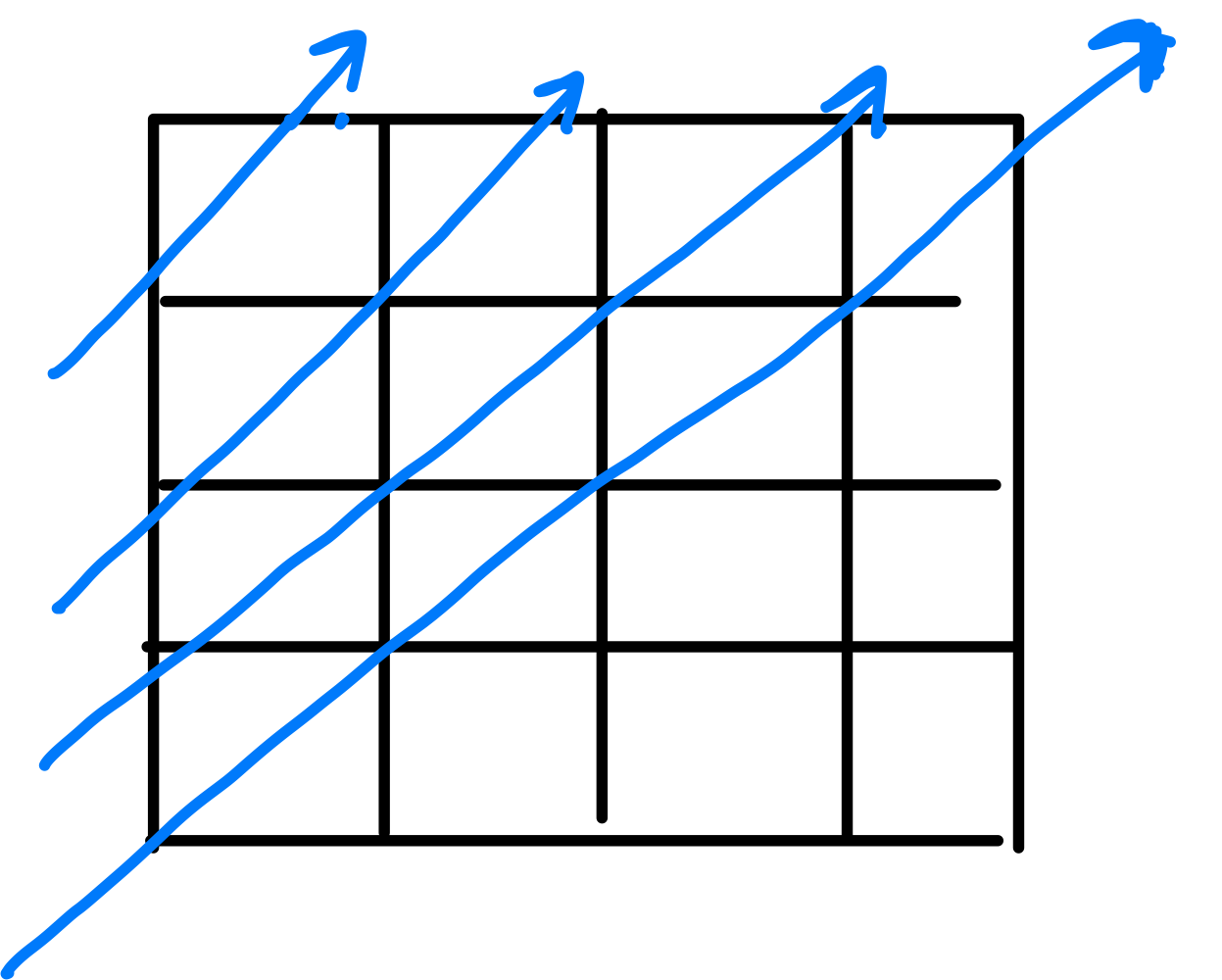
이 때, 하나의 집합에서 점을 순서대로 선택하기 위한 규칙을 다음과 같다. 왼쪽 상단부터 idx = 0이라고 하면,
- idx = 0 : (0,0)
- idx = 1 : (0,1), (1,0)
- idx = 2 : (0,2), (1,1), (2.0)
즉 x좌표는 0~idx까지의 범위에서 순차적으로 증가하고 이 때 y좌표는 idx - x가 된다. 즉, (x,idx - x)의 좌표가 해당 대각선에 속하는 점이다.
여기서 고려해야 할 점이 idx가 N을 넘어갔을 경우에는 모든 점이 다 속하는게 아니게 된다. 위의 그림에서 다음 대각선에 속하는 점을 위의 공식으로 구해보면 (0,5), (1,4), (2,3), (3,2), (4,1), (5,0)이지만 해당 배열 범위에 포함되지 않는 점도 존재한다. 따라서 이에 대한 예외처리가 필요하다.
범위에 만족하고, 놓을 수 있는 경우(현재 칸에 비숍을 놓을 수 있고 반대 방향 대각선에 비숍이 없는 경우)에는 cache[idx]를 x좌표로 갱신하고 비숍 cnt를 하나씩 증가시켜 다음 idx에 대한 검사를 수행한다. 최종적으로 idx가 대각선 개수와 같아지는 경우 maxCnt를 갱신하고 리턴하게 된다.
private static void putBishop(int idx, int cnt) {
if (idx == (2 * N) - 1) {
if (macCnt < cnt) macCnt = cnt;
return;
}
boolean isExist = false;
for (int i = 0; i <= idx; i++) {
if (i >= N || idx - i >= N || map[i][idx - i] == 0 || !isAvailable(i, idx - i, idx)) continue;
cache[idx] = i;
putBishop(idx + 1, cnt + 1);
isExist = true;
}
if (!isExist) {
cache[idx] = -1;
putBishop(idx + 1, cnt);
}
}위의 코드에서 isExist는 해당 대각선에 놓을 수 있는 점이 존재하는지 판단하는 플래그이다. 해당 대각선에 놓을 수 없는 경우에는 cnt는 그대로, cache[idx] = -1을 저장한다.
다음으로 해야할 작업은 반대 방향 대각선에 비숍이 존재하는지 확인하는 작업이다. 이에 대한 규칙은 다음과 같이 정의했다.
현재 대각선이 idx번이고 좌표가 (x,y)인 경우, 검사는 idx - 2인 대각선부터 (x-1, y-1)을 검사하면 된다. 여기서 cache에 x좌표를 저장했기 때문에 cache[idx - 2] = x -1인지를 idx가 0보다 클 때까지 반복해서 검사하면 된다.
private static boolean isAvailable(int x, int y, int idx) {
while(idx >= 2 && x >= 1 && y >= 1) {
idx -= 2;
x -= 1;
y -= 1;
if (cache[idx] == x) return false;
}
return true;
}최종 코드는 다음과 같다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Solution1799 {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static int N, macCnt;
static int[] cache;
static int[][] map;
public static void main(String[] args) throws IOException {
N = Integer.parseInt(br.readLine());
cache = new int[2 * N - 1];
map = new int[N][N];
for (int i = 0; i < N; i++) {
String[] line = br.readLine().split(" ");
for (int j = 0; j < N; j++) {
map[i][j] = Integer.parseInt(line[j]);
}
}
putBishop(0, 0);
System.out.println(macCnt);
}
private static void putBishop(int idx, int cnt) {
if (idx == (2 * N) - 1) {
if (macCnt < cnt) macCnt = cnt;
return;
}
boolean isExist = false;
for (int i = 0; i <= idx; i++) {
if (i >= N || idx - i >= N || map[i][idx - i] == 0 || !isAvailable(i, idx - i, idx)) continue;
cache[idx] = i;
putBishop(idx + 1, cnt + 1);
isExist = true;
}
if (!isExist) {
cache[idx] = -1;
putBishop(idx + 1, cnt);
}
}
private static boolean isAvailable(int x, int y, int idx) {
while(idx >= 2 && x >= 1 && y >= 1) {
idx -= 2;
x -= 1;
y -= 1;
if (cache[idx] == x) return false;
}
return true;
}
}
'🔎 Algorithm > 💻 문제 풀이' 카테고리의 다른 글
| [백준] - 2206. 벽부수고 이동하기 (0) | 2021.03.24 |
|---|---|
| [백준] - 1277. 발전소 설치 (0) | 2021.03.24 |
| [백준] 1967. 트리의 지름 (0) | 2021.03.06 |
| [백준] 1987. 알파벳 (0) | 2021.02.19 |
| [백준] 3109. 빵집 (0) | 2021.02.19 |




댓글